מבוא למדעי המחשב
|
|
|
- אוהד דוידוב
- לפני6 שנים
- צפיות:
תמליל
1 מבוא למדעי המחשב גרפים 1
2 תוכן עניינים סיכום ביניים
3 מה היה לנו? מושג האלגוריתם, תכנות פרוצדורלי הכרות עם בעיות במדעי המחשב הכרות עם בעיות ברקורסיה מתקדמת (כולל (memoization תכנות מונחה עצמים (מחלקה, הורשה, ממשקים) מבני נתונים (מערך, רשימה משורשרת, מחסנית, תור, עצים, איטראטור) נושאים במדעי המחשב,SAT) מיון וחיפוש, נוסחאות ב- (RPN מה נעשה ביתר הזמן גרפים אלגוריתמים על גרפים
4 תוכן עניינים סיכום ביניים גרפים
5 גרפים הגדרה אינטואיטיבית קבוצה של קדקודים nodes) או (vertices חלקם מקושרים זה לזה בעזרת קשתות (edges) הקשתות יכול להיות מכוונות או לא-מכוונות גרף בו הקשתות מכוונות נקרא גרף מכוון. גרף בו הקשתות לא מכוונות נקרא גרף לא מכוון בגרף לא מכוון לקשתות אין כיוון בגרף לא מכוון אין קשתות עצמיות
6 גרפים הגדרה פורמלית גרף הוא זוג סדור (VVVVV),GG = כאשר 0 VV היא קבוצה של קדקודים EE VV XX VV היא קבוצה של קשתות בין הקדקודים הנ"ל דוגמה VV = {0,1,2,3 EE = { 0,3, 1,2, 3,1,{2,3 (nn 1) לשם פשטות תמיד נניח שבגרף בן nn קדקודים הקדקודים ממוספרים בין 0 ל-
7 גרפים כמה מושגים 0 דרגה של קדקוד מספר הקשתות שנוגעות בקדקוד למשל, = 2 dddddddddddd(1) שכנים של קדקוד הקדקודים שבינם לבין הקדקוד עוברת קשת למשל, = 2,3 1 nnnnnnnnhbbbbbbbb מסלול בגרף רשימה של קדקודים שבין כל שניים עוקבים עוברת קשת למשל, > 1,2,3,0,3,1 <
8 תוכן עניינים סיכום ביניים גרפים קדקוד וקשת של גרף
9 המחלקה Edge public class Edge { public final int left; public final int right; public Edge(int left, int right) { this.left = left; this.right = right; קדקוד מיוצג פשוט על ידי מספר שלם (אובייקט מהמחלקה (Integer קשת תיוצג באמצעות המחלקה edge שמשמאל public String tostring() { return {" + left + ", " + right + ";
10 תוכן עניינים סיכום ביניים גרפים קדקוד וקשת של גרף הממשק Graph
11 public interface Graph { int numberofvertices(); int numberofedges(); boolean containsedge(int u, int v); void addedge(int u, int v); void removeedge(int u, int v); int degree(int u); Set<Integer> neighborsof(int u); Set<Edge> edgeset(); הממשק Graph
12 תוכן עניינים סיכום ביניים גרפים קדקוד וקשת של גרף הממשק Graph ייצוג של גרפים
13 ייצוג גרפים 0 שתי שיטות נפוצות (Adjacency Lists) (Adjacency Matrix) רשימות שכנים מטריצת שכנים יש שיטות נוספות Adjacency Lists Adjacency Matrix false false false true false false true true false true false true true true true false
14 תוכן עניינים סיכום ביניים גרפים קדקוד וקשת של גרף הממשק Graph ייצוג של גרפים מחלקות אבסטרקטיות
15 מחלקות אבסטרקטיות בעיה אנחנו רוצים לבנות מחלקות לגרפים בשתי צורות הייצוג שראינו מחלקה בשם GraphAsAdjacencyLists ומחלקה בשם GraphAsAdjacencyMatrix על פניו נראה שיש ביניהן (למרות השוני בייצוג) הרבה מן המשותף למשל, השיטה שמחזירה את קבוצת השכנים של קדקוד היינו רוצים לממש את השיטות האלה פעם אחת בשביל שתי המחלקות צרה צרורה על פניו לא נראה שיש בין המחלקות קשרים היררכיים אז איפה נממש? לא זו מקרה פרטי של זו ולא זו מקרה פרטי של זו
16 מחלקות אבסטרקטיות פתרון בעיה נגדיר מעליהן מחלקה שתיהן ירשו אותה ואת הקוד המשותף נממש במחלקה שמעליהן אנחנו רוצים לבנות מחלקות לגרפים בשתי צורות הייצוג שראינו מחלקה בשם GraphAsAdjacencyLists ומחלקה בשם GraphAsAdjacencyMatrix על פניו נראה שיש ביניהן הרבה מן המשותף (למרות השוני בייצוג) למשל, השיטה שמחזירה את מספר השכנים של קדקוד היינו רוצים לממש את השיטות האלה פעם אחת בשביל שתי המחלקות צרה צרורה על פניו לא נראה שיש בין המחלקות קשרים היררכיים אז איפה נממש? לא זו מקרה פרטי של זו ולא זו מקרה פרטי של זו
17 מחלקות אבסטרקטיות בעיה אבל איזה מין אובייקטים תגדיר המחלקה הזו? יצורי כילאים שאין לנו שום צורך אמתי בהם הרי הגדרנו אותה רק לצורך מחזר קוד
18 מחלקות אבסטרקטיות פתרון בעיה אז נגדיר אותה אבסטרקטית מחלקה שרק תופסת מקום בהיררכיה (לצרכים של מחזור קוד), אבל אי אפשר ליצור ממנה אובייקטים אבל איזה מין אובייקטים תגדיר המחלקה הזו? יצורי כילאים שאין לנו שום צורך אמתי בהם הרי הגדרנו אותה רק לצורך מחזר קוד
19 מחלקות אבסטרקטיות בעיה לא נראה שנוכל לממש כל מה שאנחנו רוצים במחלקה האבסטרקטית שאנחנו מתכננים חלק מהקוד בוודאי תלוי בצורת הייצוג של הגרף למשל האם שני קדקודים שכנים אולי נאלץ להשאיר בה חורים או חס וחלילה לא עלינו לאלתר סתימות מה נעשה?
20 מחלקות אבסטרקטיות פתרון בעיה כיוון שהמחלקה אבסטרקטית איננו חייבים לממש בא הכול אנחנו יכולים להשאיר חלק מהשיטות אבסטרקטיות כי בלאו הכי איננו יכולים ליצור אובייקטים מהמחלקה לא נראה שנוכל לממש כל מה שאנחנו רוצים במחלקה האבסטרקטית שאנחנו מתכננים חלק מהקוד בוודאי תלוי בצורת הייצוג של הגרף גמור זיל ואידך למשל האם שני קדקודים שכנים אולי נאלץ להשאיר בה חורים או חס וחלילה לא עלינו לאלתר סתימות מה נעשה?
21 תוכן עניינים סיכום ביניים גרפים קדקוד וקשת של גרף הממשק Graph ייצוג של גרפים מחלקות אבסטרקטיות המחלקה AbstractGraph
22 שדה ובנאי המחלקה AbstractGraph public abstract class AbstractGraph implements Graph { protected final int nvertices; public AbstractGraph(int nvertices) { this.nvertices = nvertices; public interface Graph { int numberofvertices(); int numberofedges(); boolean containsedge(int u, int v); void addedge(int u, int v); void removeedge(int u, int v); int degree(int u); Set<Integer> neighborsof(int u); Set<Edge> edgeset();
23 שיטות המחלקה AbstractGraph protected final int nvertices;... public int numberofvertices() { return nvertices; // Default implementation public int numberofedges() { return edgeset().size(); // Default implementation public int degree(int v) { return neighborsof(v).size(); public interface Graph { int numberofvertices(); int numberofedges(); boolean containsedge(int u, int v); void addedge(int u, int v); void removeedge(int u, int v); int degree(int u); Set<Integer> neighborsof(int u); Set<Edge> edgeset();
24 שיטות המחלקה AbstractGraph protected final int nvertices;... // Default implementation public Set<Integer> neighborsof(int v) { Set<Integer> adj = new SetAsLinkedList<>(); for (int u = 0; u < nvertices; u = u + 1) if (u!= v && containsedge(u, v)) adj.add(u); return adj; containsedge זורק חריגה במקרה ש- u=v (נראה בהמשך) public interface Graph { int numberofvertices(); int numberofedges(); boolean containsedge(int u, int v); void addedge(int u, int v); void removeedge(int u, int v); int degree(int u); Set<Integer> neighborsof(int u); Set<Edge> edgeset(); c
25 שיטות המחלקה AbstractGraph protected final int nvertices;... // Default implementation public Set<Edge> edgeset() { Set<Edge> edges = new SetAsLinkedList<>(); for (int u = 0; u < nvertices - 1; u = u + 1) for (int v = u + 1; v < nvertices; v = v + 1) if (containsedge(u, v)) edges.add(new Edge(u, v)); return edges; public interface Graph { int numberofvertices(); int numberofedges(); boolean containsedge(int u, int v); void addedge(int u, int v); void removeedge(int u, int v); int degree(int u); Set<Integer> neighborsof(int u); Set<Edge> edgeset();
26 שיטות המחלקה AbstractGraph protected final int nvertices;... public String tostring() { return "G=([" ".. " + (nvertices - 1) + "], " + edgeset() + ")"; public interface Graph { int numberofvertices(); int numberofedges(); boolean containsedge(int u, int v); void addedge(int u, int v); void removeedge(int u, int v); int degree(int u); Set<Integer> neighborsof(int u); Set<Edge> edgeset();
27 שיטות המחלקה AbstractGraph protected final int nvertices;... public boolean equals(object x) { if (!(x instanceof Graph)) return false; Graph other = (Graph) x; return this.nvertices == other.numberofvertices() && this.edgeset().equals(other.edgeset()); public interface Graph { int numberofvertices(); int numberofedges(); boolean containsedge(int u, int v); void addedge(int u, int v); void removeedge(int u, int v); int degree(int u); Set<Integer> neighborsof(int u); Set<Edge> edgeset();
28 שיטות המחלקה AbstractGraph protected final int nvertices;... public abstract boolean containsedge(int u, int v); public abstract void addedge(int u, int v); public abstract void removeedge(int u, int v); לא חובה להכריז, הן כבר מוכרזות בממשק public interface Graph { int numberofvertices(); int numberofedges(); boolean containsedge(int u, int v); void addedge(int u, int v); void removeedge(int u, int v); int degree(int u); Set<Integer> neighborsof(int u); Set<Edge> edgeset();
29 שיטות המחלקה AbstractGraph protected final int nvertices;... protected boolean edgecheck(int u, int v) { return u >= 0 && u < nvertices && v >= 0 && v < nvertices && u!= v; public interface Graph { int numberofvertices(); int numberofedges(); boolean containsedge(int u, int v); void addedge(int u, int v); void removeedge(int u, int v); int degree(int u); Set<Integer> neighborsof(int u); Set<Edge> edgeset();
30 תוכן עניינים סיכום ביניים גרפים קדקוד וקשת של גרף הממשק Graph ייצוג של גרפים מחלקות אבסטרקטיות המחלקה AbstractGraph המחלקה GraphAsAdjacencyMatrix
31 שדה המחלקה GraphAsAdjacencyMatrix ובנאי פשוט public class GraphAsAdjacencyMatrix extends AbstractGraph { private boolean[][] edges; public GraphAsAdjacencyMatrix(int nvertices) { super(nvertices); edges = new boolean[nvertices][nvertices]; public interface Graph { int numberofvertices(); int numberofedges(); boolean containsedge(int u, int v); void addedge(int u, int v); void removeedge(int u, int v); int degree(int u); Set<Integer> neighborsof(int u); Set<Edge> edgeset();
32 המחלקה GraphAsAdjacencyMatrix בנאי מעתיק private boolean[][] edges;... public GraphAsAdjacencyMatrix(Graph other) { this(other.numberofvertices()); Set<Edge> otheredges = other.edgeset(); for (Edge e : otheredges) addedge(e.left, e.right); public interface Graph { int numberofvertices(); int numberofedges(); boolean containsedge(int u, int v); void addedge(int u, int v); void removeedge(int u, int v); int degree(int u); Set<Integer> neighborsof(int u); Set<Edge> edgeset();
33 שיטות המחלקה GraphAsAdjacencyMatrix private boolean[][] edges;... public boolean containsedge(int u, int v) { if (!edgecheck(u, v)) throw new IllegalArgumentException(); return edges[u][v]; public interface Graph { int numberofvertices(); int numberofedges(); boolean containsedge(int u, int v); void addedge(int u, int v); void removeedge(int u, int v); int degree(int u); Set<Integer> neighborsof(int u); Set<Edge> edgeset();
34 שיטות המחלקה GraphAsAdjacencyMatrix private boolean[][] edges;... public void addedge(int u, int v) { if (!edgecheck(u, v)) throw new IllegalArgumentException(); edges[u][v] = true; edges[v][u] = true; public interface Graph { int numberofvertices(); int numberofedges(); boolean containsedge(int u, int v); void addedge(int u, int v); void removeedge(int u, int v); int degree(int u); Set<Integer> neighborsof(int u); Set<Edge> edgeset();
35 שיטות המחלקה GraphAsAdjacencyMatrix private boolean[][] edges;... public void removeedge(int u, int v) { if (!edgecheck(u, v)) throw new IllegalArgumentException(); edges[u][v] = false; edges[v][u] = false; public interface Graph { int numberofvertices(); int numberofedges(); boolean containsedge(int u, int v); void addedge(int u, int v); void removeedge(int u, int v); int degree(int u); Set<Integer> neighborsof(int u); Set<Edge> edgeset();
36 תוכן עניינים סיכום ביניים גרפים קדקוד וקשת של גרף הממשק Graph ייצוג של גרפים מחלקות אבסטרקטיות המחלקה AbstractGraph המחלקה GraphAsAdjacencyMatrix המחלקה GraphAlgorithm
37 המחלקה האבסטרקטית GraphAlgorithm כדי לפעול על גרפים נגדיר מחלקה אבסטרקטית שתשמש כאופרטור של גרפים הבנאי מקבל כפרמטר את הגרף האלגוריתם ממומש על ידי דריסה של השיטה האבסטרקטית runalgorithm מחלקה אחת יכולה לממש אלגוריתם לבדיקת קשירות של גרף מחלקה אחרת יכולה לממש אלגוריתם שבודק אם יש מעגלים בגרף public abstract class GraphAlgorithm { protected Graph g; public GraphAlgorithm(Graph g) { this.g = g; public abstract Object runalgorithm();
38 המחלקה EvenDegreesAlgorithm מרחיבה את GraphAlgorithm ומגדירה אובייקט שבודק אם הדרגה של גרף נתון היא זוגית (דרגת כל הקדקודים בגרף זוגית) public class EvenDegreesAlgorithm extends GraphAlgorithm { public EvenDegreesAlgorithm(Graph g) { super(g); public Object runalgorithm() { for (int u = 0; u < g.numberofvertices(); u = u + 1) if (g.degree(u) % 2!= 0) return false; return true;
39 תוכן עניינים סיכום ביניים גרפים קדקוד וקשת של גרף הממשק Graph ייצוג של גרפים מחלקות אבסטרקטיות המחלקה AbstractGraph המחלקה GraphAsAdjacencyMatrix המחלקה GraphAlgorithm קשירות
40 קשירות נאמר שגרף הוא קשיר אם בין כל זוג קדקודים בגרף עובר מסלול לא קשיר קשיר
41 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
42 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
43 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
44 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
45 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
46 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
47 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
48 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
49 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
50 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
51 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
52 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
53 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
54 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
55 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
56 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
57 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
58 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
59 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
60 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
61 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
62 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
63 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
64 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
65 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
66 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
67 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
68 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
69 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
70 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
71 בדיקת קשירות של גרף נתחיל את הבדיקה מקדקוד כלשהו (נניח קדקוד 0) ואז ברקורסיה בסיום נסמן שביקרנו בו נסרוק את שכניו עבור כל שכן שעדיין לא ביקרנו בו (לא סומן) נתחיל ברקורסיה בדיקה חדשה מהשכן הזה אם כל הקדקודים סומנו הגרף קשיר אחרת הגרף לא קשיר
72 תוכן עניינים סיכום ביניים גרפים קדקוד וקשת של גרף הממשק Graph ייצוג של גרפים מחלקות אבסטרקטיות המחלקה AbstractGraph המחלקה GraphAsAdjacencyMatrix המחלקה GraphAlgorithm קשירות המחלקה ConnectivityAlgorithm
73 private boolean isreachedall(boolean[] visited) { for (boolean isvisited : visited) if (!isvisited) return false; return true; המחלקה ConnectivityAlgorithm מרחיבה את GraphAlgorithm ומגדירה אובייקט שבודק אם גרף נתון הוא גרף קשיר public class ConnectivityAlgorithm extends GraphAlgorithm { public ConnectivityAlgorithm(Graph g) { super(g); public Object runalgorithm() { boolean[] visited = new boolean[g.numberofvertices()]; dfs(0, visited); return isreachedall(visited); private void dfs(int u, boolean[] visited) { visited[u] = true; for (Integer v : g.neighborsof(u)) if (!visited[v]) dfs(v, visited);
74 דוגמת הרצה public static void main(string[] args) { Graph g = new GraphAsAdjacencyMatrix(10); for (int u = 0; u < g.numberofvertices(); u = u + 1) g.addedge(u, (u + 1) % g.numberofvertices()); System.out.println(g); GraphAlgorithm ca = new ConnectivityAlgorithm(g); System.out.println(ca.runAlgorithm()); // true g.removeedge(0, 1); System.out.println(ca.runAlgorithm()); // true g.removeedge(4, 5); System.out.println(ca.runAlgorithm()); // false
75 תוכן עניינים סיכום ביניים גרפים קדקוד וקשת של גרף הממשק Graph ייצוג של גרפים מחלקות אבסטרקטיות המחלקה AbstractGraph המחלקה GraphAsAdjacencyMatrix המחלקה GraphAlgorithm קשירות המחלקה ConnectivityAlgorithm המבנים שראינו
76 המבנים שראינו ושניראה בהמשך interface: Graph implements GraphAlgorithm extends AbstractGraph EvenDegreesAlgorithm extends ConnectivityAlgorothm GraphAsAdjacencyMatrix EulerPathAlgorithm GraphAsAdjacencyLists
מבוא למדעי המחשב
 מבוא למדעי המחשב המחלקה Object תוכן עניינים Object הורשה והמחלקה ערך שם טיפוס DynamicIntArray da data size incrementsize DynamicArray תזכורת - Object[] data; int size; int incrementsize; DynamicArray זה
מבוא למדעי המחשב המחלקה Object תוכן עניינים Object הורשה והמחלקה ערך שם טיפוס DynamicIntArray da data size incrementsize DynamicArray תזכורת - Object[] data; int size; int incrementsize; DynamicArray זה
Slide 1
 מבוא למדעי המחשב משפחות של מחלקות ומחלקות מופשטות תזכורת בשיעור הקודם ראינו מחלקה של Student והרחבה שלה למחלקה של Milgae למעשה Student יכול לעמוד בראש היררכיה שלמה של מחלקות שונות של סטודנטים למשל, בנוסף
מבוא למדעי המחשב משפחות של מחלקות ומחלקות מופשטות תזכורת בשיעור הקודם ראינו מחלקה של Student והרחבה שלה למחלקה של Milgae למעשה Student יכול לעמוד בראש היררכיה שלמה של מחלקות שונות של סטודנטים למשל, בנוסף
מבוא למדעי המחשב
 מבוא למדעי המחשב שימוש במחסנית - מחשבון תוכן עניינים prefix כתיבת ביטויים ב-,infix ו- postfix postfix prefix,infix ביטויים ב- כתיבת ו- infix נוסח כתיבה ב- (operator אנו רגילים לכתוב ביטויים חשבוניים כדוגמת
מבוא למדעי המחשב שימוש במחסנית - מחשבון תוכן עניינים prefix כתיבת ביטויים ב-,infix ו- postfix postfix prefix,infix ביטויים ב- כתיבת ו- infix נוסח כתיבה ב- (operator אנו רגילים לכתוב ביטויים חשבוניים כדוגמת
מבוא למדעי המחשב
 מבוא למדעי המחשב תכנות מונחה אובייקטים תוכן עניינים טיפוסי נתונים מורכבים המחלקה String תזכורת לשימוש שעשינו במחלקה String str = new String( Hello ); s.o.p(str.tostring()); s.o.p(str.charat(4)); s.o.p(str.equals(
מבוא למדעי המחשב תכנות מונחה אובייקטים תוכן עניינים טיפוסי נתונים מורכבים המחלקה String תזכורת לשימוש שעשינו במחלקה String str = new String( Hello ); s.o.p(str.tostring()); s.o.p(str.charat(4)); s.o.p(str.equals(
מבוא למדעי המחשב
 מבוא למדעי המחשב הממשקים Iterable,Set ו- Iterator תוכן עניינים מבנה נתונים מבנה נתונים מבנה נתונים הוא container של עצמים שמוגדרות עליו מספר פעולות למשל קבוצה של עצמים (אוסף ללא חזרות) עם הפעולות: הוספת
מבוא למדעי המחשב הממשקים Iterable,Set ו- Iterator תוכן עניינים מבנה נתונים מבנה נתונים מבנה נתונים הוא container של עצמים שמוגדרות עליו מספר פעולות למשל קבוצה של עצמים (אוסף ללא חזרות) עם הפעולות: הוספת
אוניברסיטת בן גוריון בנגב תאריך המבחן: שקולניק אלכסנדר שם המרצה: מר בשפת JAVA מבוא לתכנות מבחן ב: מס' הקורס : הנדסת תעשיה וניהול מ
 אוניברסיטת בן גוריון בנגב תאריך המבחן: 12.02.17 שקולניק אלכסנדר שם המרצה: מר בשפת JAVA מבוא לתכנות מבחן ב: 202.1.9031 מס' הקורס : הנדסת תעשיה וניהול מיועד לתלמידי : א' מועד א' סמ' שנה תשע"ד 3 שעות משך
אוניברסיטת בן גוריון בנגב תאריך המבחן: 12.02.17 שקולניק אלכסנדר שם המרצה: מר בשפת JAVA מבוא לתכנות מבחן ב: 202.1.9031 מס' הקורס : הנדסת תעשיה וניהול מיועד לתלמידי : א' מועד א' סמ' שנה תשע"ד 3 שעות משך
תרגול 1
 מבוא למדעי המחשב 2019 תרגול 12 מחסנית )Stack( memoization ראינו בהרצאה מחסנית Infix/Postfix Notations בתרגול היום מחסנית בדיקת איזון סוגריים בביטוי אריתמטי מימוש תור באמצעות מחסנית memoization דוגמאות
מבוא למדעי המחשב 2019 תרגול 12 מחסנית )Stack( memoization ראינו בהרצאה מחסנית Infix/Postfix Notations בתרגול היום מחסנית בדיקת איזון סוגריים בביטוי אריתמטי מימוש תור באמצעות מחסנית memoization דוגמאות
Slide 1
 בית הספר למדעי המחשב אוניברסיטת תל אביב תוכנה 1- תרגול הורשה מחלקות אבסטרקטיות חריגים 2 ירושה ממחלקות קיימות ראינו בהרצאה שתי דרכים לשימוש חוזר בקוד של מחלקה קיימת: הכלה + האצלה הכלה )aggregation( במחלקה
בית הספר למדעי המחשב אוניברסיטת תל אביב תוכנה 1- תרגול הורשה מחלקות אבסטרקטיות חריגים 2 ירושה ממחלקות קיימות ראינו בהרצאה שתי דרכים לשימוש חוזר בקוד של מחלקה קיימת: הכלה + האצלה הכלה )aggregation( במחלקה
מבוא לתכנות ב- JAVA תרגול 11
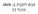 מבוא לתכנות ב- JAVA תרגול 11 רשימה מקושרת אוסף סדור של איברים מאותו טיפוס. קודקוד ברשימה )Node( מכיל את המידע + הצבעה לקודקוד הבא ברשימה data next first רשימה :)List( מיוצגת ע"י מצביע לאיבר הראשון ברשימה
מבוא לתכנות ב- JAVA תרגול 11 רשימה מקושרת אוסף סדור של איברים מאותו טיפוס. קודקוד ברשימה )Node( מכיל את המידע + הצבעה לקודקוד הבא ברשימה data next first רשימה :)List( מיוצגת ע"י מצביע לאיבר הראשון ברשימה
אוניברסיטת בן גוריון בנגב תאריך המבחן: שם המרצה: מר אלכסנדר שקולניק, בשפת JAVA מבחן ב: מבוא לתכנות מס' הקורס : מיועד לתלמידי : הנד
 אוניברסיטת בן גוריון בנגב תאריך המבחן: 29.01.19 שם המרצה: מר אלכסנדר שקולניק, בשפת JAVA מבחן ב: מבוא לתכנות 202.1.9031 מס' הקורס : מיועד לתלמידי : הנדסת תעשיה וניהול שנה תשע"ט א' סמ' א' מועד 3 שעות משך
אוניברסיטת בן גוריון בנגב תאריך המבחן: 29.01.19 שם המרצה: מר אלכסנדר שקולניק, בשפת JAVA מבחן ב: מבוא לתכנות 202.1.9031 מס' הקורס : מיועד לתלמידי : הנדסת תעשיה וניהול שנה תשע"ט א' סמ' א' מועד 3 שעות משך
תרגול 1
 מבוא למדעי המחשב 2019 תרגול 9 חזרה על תכנות מונחה עצמים Part II ראינו בהרצאה ממשקים Set Iterable Iterator בתרגול היום חזרה על: ממשקים Iterator Iterable )iterator נראה: )set ממשק )מימוש SetAsLinkedList
מבוא למדעי המחשב 2019 תרגול 9 חזרה על תכנות מונחה עצמים Part II ראינו בהרצאה ממשקים Set Iterable Iterator בתרגול היום חזרה על: ממשקים Iterator Iterable )iterator נראה: )set ממשק )מימוש SetAsLinkedList
מקביליות
 תכונות שמורה Invariant Properties גרא וייס המחלקה למדעי המחשב אוניברסיטת בן-גוריון 2 בדיקות מודל Checking( )Model מערכת דרישות מידול פירמול בדיקות מודל )Model Checking( מודל של המערכת תכונות פורמליות סימולציה
תכונות שמורה Invariant Properties גרא וייס המחלקה למדעי המחשב אוניברסיטת בן-גוריון 2 בדיקות מודל Checking( )Model מערכת דרישות מידול פירמול בדיקות מודל )Model Checking( מודל של המערכת תכונות פורמליות סימולציה
פקולטה: מחלקה: שם הקורס: קוד הקורס: מדעי הטבע מדעי המחשב ומתמטיקה מתמטיקה בדידה תאריך בחינה: _ 07/07/2015 משך הבחינה: 3 שעות סמ' _ב' מועד
 פקולטה: מחלקה: שם הקורס: קוד הקורס: מדעי הטבע מדעי המחשב ומתמטיקה מתמטיקה בדידה 2-7012610-3 תאריך בחינה: _ 07/07/2015 משך הבחינה: 3 שעות סמ' _ב' מועד ב' שם המרצה: ערן עמרי, ענת פסקין-צ'רניאבסקי חומר עזר:
פקולטה: מחלקה: שם הקורס: קוד הקורס: מדעי הטבע מדעי המחשב ומתמטיקה מתמטיקה בדידה 2-7012610-3 תאריך בחינה: _ 07/07/2015 משך הבחינה: 3 שעות סמ' _ב' מועד ב' שם המרצה: ערן עמרי, ענת פסקין-צ'רניאבסקי חומר עזר:
תכנון אלגוריתמים עבודת בית 4: תכנון אלגוריתמים תאריך הגשה: 02: , בצהריים,תא מספר 66 בקומת כניסה של בניין 003 מתרגל אחראי: אורי 0
 22 עבודת בית 4: תכנון אלגוריתמים תאריך הגשה: 2: 622, בצהריים,תא מספר 66 בקומת כניסה של בניין 3 מתרגל אחראי: אורי הוראות כלליות: כל עוד לא נאמר אחרת, כאשר הנכם מתבקשים לתאר אלגוריתם יש לספק את הבאות: תיאור
22 עבודת בית 4: תכנון אלגוריתמים תאריך הגשה: 2: 622, בצהריים,תא מספר 66 בקומת כניסה של בניין 3 מתרגל אחראי: אורי הוראות כלליות: כל עוד לא נאמר אחרת, כאשר הנכם מתבקשים לתאר אלגוריתם יש לספק את הבאות: תיאור
מבחן 7002 פרטים כלליים מועד הבחינה: בכל זמן מספר השאלון: 1 משך הבחינה: 3 שעות חומר עזר בשימוש: הכל )ספרים ומחברות( המלצות: קרא המלצות לפני הבחינה ובדי
 מבחן 7002 פרטים כלליים מועד הבחינה: בכל זמן מספר השאלון: 1 משך הבחינה: 3 שעות חומר עזר בשימוש: הכל )ספרים ומחברות( המלצות: קרא המלצות לפני הבחינה ובדיקות אחרונות לפני מסירה )עמודים 8-11( מבנה השאלון 5
מבחן 7002 פרטים כלליים מועד הבחינה: בכל זמן מספר השאלון: 1 משך הבחינה: 3 שעות חומר עזר בשימוש: הכל )ספרים ומחברות( המלצות: קרא המלצות לפני הבחינה ובדיקות אחרונות לפני מסירה )עמודים 8-11( מבנה השאלון 5
הטכניון מכון טכנולוגי לישראל אלגוריתמים 1 )443432( סמסטר חורף הפקולטה למדעי המחשב תרגול 9 מסלולים קלים ביותר תרגיל APSP - 1 עד כה דנו באלגור
 תרגול 9 מסלולים קלים ביותר תרגיל APSP - 1 עד כה דנו באלגוריתמים לפתרון בעית מסלולים קלים מציאת מסלולים קלים ביותר מצומת ביותר ממקור יחיד. כלומר, V לכל צמתי הגרף. בעיה אחרת הקשורה לבעיה זו היא בעית ה-(
תרגול 9 מסלולים קלים ביותר תרגיל APSP - 1 עד כה דנו באלגוריתמים לפתרון בעית מסלולים קלים מציאת מסלולים קלים ביותר מצומת ביותר ממקור יחיד. כלומר, V לכל צמתי הגרף. בעיה אחרת הקשורה לבעיה זו היא בעית ה-(
תרגול 1
 מבוא למדעי המחשב 2019 תרגול 9 חזרה על תכנות מונחה עצמים Part II ראינו בהרצאה ממשקים Set Iterable Iterator בתרגול היום חזרה על: ממשקים Iterator Iterable )iterator נראה: )set ממשק )מימוש SetAsLinkedList
מבוא למדעי המחשב 2019 תרגול 9 חזרה על תכנות מונחה עצמים Part II ראינו בהרצאה ממשקים Set Iterable Iterator בתרגול היום חזרה על: ממשקים Iterator Iterable )iterator נראה: )set ממשק )מימוש SetAsLinkedList
מספר זהות: סמסטר ב' מועד א' תאריך: 11102/4// שעה: 9:22 משך הבחינה: 3 שעות חומר עזר: אין מותר השימוש במחשבון פשוט בחינה בקורס: מבני נתונים מרצה: הדר בי
 מספר זהות: סמסטר ב' מועד א' תאריך: 11102/4// שעה: 9:22 משך הבחינה: 3 שעות חומר עזר: אין מותר השימוש במחשבון פשוט בחינה בקורס: מבני נתונים מרצה: הדר בינסקי הנחיות: יש לענות על כל השאלות. יש לענות על כל
מספר זהות: סמסטר ב' מועד א' תאריך: 11102/4// שעה: 9:22 משך הבחינה: 3 שעות חומר עזר: אין מותר השימוש במחשבון פשוט בחינה בקורס: מבני נתונים מרצה: הדר בינסקי הנחיות: יש לענות על כל השאלות. יש לענות על כל
Slide 1
 בית הספר למדעי המחשב אוניברסיטת תל אביב תוכנה 1 תרגול מספר 9: הורשה מחלקות אבסטרקטיות ואתחול עצמים 2 ירושה ממחלקות קיימות ראינו בהרצאה שתי דרכים לשימוש חוזר בקוד של מחלקה קיימת: הכלה + האצלה הכלה כאשר
בית הספר למדעי המחשב אוניברסיטת תל אביב תוכנה 1 תרגול מספר 9: הורשה מחלקות אבסטרקטיות ואתחול עצמים 2 ירושה ממחלקות קיימות ראינו בהרצאה שתי דרכים לשימוש חוזר בקוד של מחלקה קיימת: הכלה + האצלה הכלה כאשר
מבוא למדעי המחשב
 מבוא למדעי המחשב מחרוזות, חתימה של פונקציה ומעטפות תוכן עניינים טיפוסים מורכבים טיפוסים מורכבים ערך שם טיפוס 12 m int undef. x boolean true y boolean arr int[] כאלה שעשויים להכיל יותר מערך פרימיטיבי אחד
מבוא למדעי המחשב מחרוזות, חתימה של פונקציה ומעטפות תוכן עניינים טיפוסים מורכבים טיפוסים מורכבים ערך שם טיפוס 12 m int undef. x boolean true y boolean arr int[] כאלה שעשויים להכיל יותר מערך פרימיטיבי אחד
עוצמת ההורשה מה הופך את ההורשה לכלי כל כך עוצמתי? מעבר לכך שהוא מקל בהגדרת מחלקות חדשות על סמך מחלקות קיימות, יש לנו אפשרות להתייחס לאובייקט מסויים בכ
 עוצמת ההורשה מה הופך את ההורשה לכלי כל כך עוצמתי? מעבר לכך שהוא מקל בהגדרת מחלקות חדשות על סמך מחלקות קיימות, יש לנו אפשרות להתייחס לאובייקט מסויים בכמה אופנים. בואו ניקח מחלקת צעצוע. אנחנו מעונינים להגדיר
עוצמת ההורשה מה הופך את ההורשה לכלי כל כך עוצמתי? מעבר לכך שהוא מקל בהגדרת מחלקות חדשות על סמך מחלקות קיימות, יש לנו אפשרות להתייחס לאובייקט מסויים בכמה אופנים. בואו ניקח מחלקת צעצוע. אנחנו מעונינים להגדיר
Slide 1
 1 אובייקטים היום בתרגול: 2.)objects מחלקות )classes( ואובייקטים )מופעים, )fields( שדות המחלקה שיטות הכמסה )methods של מחלקה. ( class מחלקה - עד עכשיו השתמשנו בעיקר בטיפוסים מובנים ופונקציות המבצעות חישובים
1 אובייקטים היום בתרגול: 2.)objects מחלקות )classes( ואובייקטים )מופעים, )fields( שדות המחלקה שיטות הכמסה )methods של מחלקה. ( class מחלקה - עד עכשיו השתמשנו בעיקר בטיפוסים מובנים ופונקציות המבצעות חישובים
Microsoft Word - ExamA_Final_Solution.docx
 סמסטר חורף תשע"א 18 בפבואר 011 הטכניון מכון טכנולוגי לישראל הפקולטה למדעי המחשב מרצה: מתרגלים: רן אל-יניב נועה אלגרבלי, גיא חפץ, נטליה זילברשטיין, דודו ינאי (אחראי) סמסטר חורף תשע" מבחן סופי פתרון (מועד
סמסטר חורף תשע"א 18 בפבואר 011 הטכניון מכון טכנולוגי לישראל הפקולטה למדעי המחשב מרצה: מתרגלים: רן אל-יניב נועה אלגרבלי, גיא חפץ, נטליה זילברשטיין, דודו ינאי (אחראי) סמסטר חורף תשע" מבחן סופי פתרון (מועד
Algorithms Tirgul 1
 - מעגלי אוילר ומסלולי אוילר תרגול 1 חידה: האם אפשר לצייר את הציורים הבאים בלי להרים את העיפרון מהנייר? 1 קצת אדמיניסטרציה אופיר פרידלר ophir.friedler@gmail.com אילן כהן - ilanrcohen@gmail.com שעות קבלה
- מעגלי אוילר ומסלולי אוילר תרגול 1 חידה: האם אפשר לצייר את הציורים הבאים בלי להרים את העיפרון מהנייר? 1 קצת אדמיניסטרציה אופיר פרידלר ophir.friedler@gmail.com אילן כהן - ilanrcohen@gmail.com שעות קבלה
לנץ קרן מרצה: תכנותמונחהעצמים) ( יוםשישי 15 אוקטובר 0202 ב מועד 0202, אביב סמסטר סמסטר סוף מבחן גוטמן אייל רביב, אריאל משנה, אלון מתרגלים: הנחי
 לנץ קרן מרצה: תכנותמונחהעצמים) 027622 ( יוםשישי 15 אוקטובר 0202 ב מועד 0202, אביב סמסטר סמסטר סוף מבחן גוטמן אייל רביב, אריאל משנה, אלון מתרגלים: הנחיות:.1.2.3.4.5.6.7 השאלות. כל על לענות עליכם משקל. שוות
לנץ קרן מרצה: תכנותמונחהעצמים) 027622 ( יוםשישי 15 אוקטובר 0202 ב מועד 0202, אביב סמסטר סמסטר סוף מבחן גוטמן אייל רביב, אריאל משנה, אלון מתרגלים: הנחיות:.1.2.3.4.5.6.7 השאלות. כל על לענות עליכם משקל. שוות
תרגול 1
 מבוא למדעי המחשב 2019 תרגול 5 מחרוזות, חתימות ורקורסיה מחרוזות רצף של תווים רקורסיה קריאה של מתודה לעצמה באופן ישיר או עקיף ראינו בהרצאה מחרוזות: תווים, חתימות: העמסה- String,הצהרה, overloading אתחול רקורסיה:
מבוא למדעי המחשב 2019 תרגול 5 מחרוזות, חתימות ורקורסיה מחרוזות רצף של תווים רקורסיה קריאה של מתודה לעצמה באופן ישיר או עקיף ראינו בהרצאה מחרוזות: תווים, חתימות: העמסה- String,הצהרה, overloading אתחול רקורסיה:
מבוא לתכנות ב- JAVA תרגול 7
 מבוא לתכנות ב- JAVA תרגול 8 תזכורת - מבנה של פונקציה רקורסיבית.2 פונקציה רקורסיבית מורכבת משני חלקים עיקריים 1. תנאי עצירה: מקרה/מקרים פשוטים בהם התוצאה לא מצריכה קריאה רקורסיבית לחישוב צעד רקורסיבי: קריאה
מבוא לתכנות ב- JAVA תרגול 8 תזכורת - מבנה של פונקציה רקורסיבית.2 פונקציה רקורסיבית מורכבת משני חלקים עיקריים 1. תנאי עצירה: מקרה/מקרים פשוטים בהם התוצאה לא מצריכה קריאה רקורסיבית לחישוב צעד רקורסיבי: קריאה
מקביליות
 תכונות בטיחות Safety Properties גרא וייס המחלקה למדעי המחשב אוניברסיטת בן-גוריון 2 תזכורת: תכונות זמן ליניארי Linear Time Properties תכונות זמן-ליניארי מתארות קבוצת עקבות שהמערכת צריכה לייצר מכוונים ללוגיקה
תכונות בטיחות Safety Properties גרא וייס המחלקה למדעי המחשב אוניברסיטת בן-גוריון 2 תזכורת: תכונות זמן ליניארי Linear Time Properties תכונות זמן-ליניארי מתארות קבוצת עקבות שהמערכת צריכה לייצר מכוונים ללוגיקה
תרגול מס' 4: המתרגם שימוש במחלקות קיימות מחרוזות, קבצים, וקבלת קלט מהמשתמש
 תרגול מס' 4: המתרגם שימוש במחלקות קיימות מחרוזות, קבצים, וקבלת קלט מהמשתמש המתרגם משימה: תכנית המתרגמת קטעי טקסט לשפה אחרת הקלט: קובץ המכיל את קטעי הטקסט וכן את השפה אליה רוצים לתרגם 2 שאלות האם כבר יש
תרגול מס' 4: המתרגם שימוש במחלקות קיימות מחרוזות, קבצים, וקבלת קלט מהמשתמש המתרגם משימה: תכנית המתרגמת קטעי טקסט לשפה אחרת הקלט: קובץ המכיל את קטעי הטקסט וכן את השפה אליה רוצים לתרגם 2 שאלות האם כבר יש
PowerPoint Presentation
 תכנות מתקדם בשפת Java אוניברסיטת תל אביב 1 תוכנה 1 תרגול 3: עבודה עם מחרוזות )Strings( מתודות )Methods( 1 תכנות מתקדם בשפת Java אוניברסיטת תל אביב 2 מחרוזות )STRINGS( 3 מחרוזות String s = Hello ; מחרוזות
תכנות מתקדם בשפת Java אוניברסיטת תל אביב 1 תוכנה 1 תרגול 3: עבודה עם מחרוזות )Strings( מתודות )Methods( 1 תכנות מתקדם בשפת Java אוניברסיטת תל אביב 2 מחרוזות )STRINGS( 3 מחרוזות String s = Hello ; מחרוזות
אוניברסיטת חיפה החוג למדעי המחשב מבוא למדעי המחשב מועד א' סמסטר ב', תשע"ג, משך המבחן: שעתיים וחצי חומר עזר: אסור הנחיות: וודאו כי יש בידיכם
 אוניברסיטת חיפה החוג למדעי המחשב מבוא למדעי המחשב מועד א' סמסטר ב', תשע"ג,.6.013 משך המבחן: שעתיים וחצי חומר עזר: אסור הנחיות: וודאו כי יש בידיכם 8 עמודי שאלון )כולל עמוד זה(. עליכם לכתוב את התשובות על
אוניברסיטת חיפה החוג למדעי המחשב מבוא למדעי המחשב מועד א' סמסטר ב', תשע"ג,.6.013 משך המבחן: שעתיים וחצי חומר עזר: אסור הנחיות: וודאו כי יש בידיכם 8 עמודי שאלון )כולל עמוד זה(. עליכם לכתוב את התשובות על
PowerPoint Presentation
 תוכנה 1 תרגול 1: סביבת העבודה ומבוא ל- Java אלכסיי זגלסקי ויעל אמסטרדמר 1 בירוקרטיה אלכסיי זגלסקי שעת קבלה: שני 13:00-14:00, בתיאום מראש משרד: בניין הנדסת תוכנה, חדר 209 יעל אמסטרדמר שעת קבלה: חמישי 15:00-16:00,
תוכנה 1 תרגול 1: סביבת העבודה ומבוא ל- Java אלכסיי זגלסקי ויעל אמסטרדמר 1 בירוקרטיה אלכסיי זגלסקי שעת קבלה: שני 13:00-14:00, בתיאום מראש משרד: בניין הנדסת תוכנה, חדר 209 יעל אמסטרדמר שעת קבלה: חמישי 15:00-16:00,
מבחן סוף סמסטר מועד א 15/02/08 מרצה אחראית: דר שירלי הלוי גינסברג מתרגלים: גלעד קותיאל, דניאל גנקין הוראות: א. בטופס המבחן 7 עמודים ו 4 דפי נוסחאות. ב
 מבחן סוף סמסטר מועד א 15/02/08 מרצה אחראית: דר שירלי הלוי גינסברג מתרגלים: גלעד קותיאל, דניאל גנקין הוראות: א. בטופס המבחן 7 עמודים ו 4 דפי נוסחאות. בדקו שכל העמודים ברשותכם. ב. משך המבחן שלוש שעות (180
מבחן סוף סמסטר מועד א 15/02/08 מרצה אחראית: דר שירלי הלוי גינסברג מתרגלים: גלעד קותיאל, דניאל גנקין הוראות: א. בטופס המבחן 7 עמודים ו 4 דפי נוסחאות. בדקו שכל העמודים ברשותכם. ב. משך המבחן שלוש שעות (180
יוםראשון, 02 ליולי 2014 סמסטר סוף מבחן )236703( עצמים מונחה תכנות - א' מועד 2014, אביב סמסטר קמחי יחיאל ד"ר מרצה: מסינג מיטל עבדאלקאדר, כרם גלעד, ערן
 יוםראשון, 02 ליולי 2014 סמסטר סוף מבחן )236703( עצמים מונחה תכנות - א' מועד 2014, אביב סמסטר קמחי יחיאל ד"ר מרצה: מסינג מיטל עבדאלקאדר, כרם גלעד, ערן מתרגלים: הנחיות: השאלות. כל על לענות עליכם משקל. שוות
יוםראשון, 02 ליולי 2014 סמסטר סוף מבחן )236703( עצמים מונחה תכנות - א' מועד 2014, אביב סמסטר קמחי יחיאל ד"ר מרצה: מסינג מיטל עבדאלקאדר, כרם גלעד, ערן מתרגלים: הנחיות: השאלות. כל על לענות עליכם משקל. שוות
Slide 1
 מבוא לתכנות ב- JAVA תרגול 5 מה בתרגול מחרוזות מערכים דו ממדיים מחרוזות (Strings) מחרוזת היא רצף של תווים. immutable על מנת ליצור ולטפל במחרוזות נשתמש במחלקה String למחלקה String מתודות שונות שמאפשרות פעולות
מבוא לתכנות ב- JAVA תרגול 5 מה בתרגול מחרוזות מערכים דו ממדיים מחרוזות (Strings) מחרוזת היא רצף של תווים. immutable על מנת ליצור ולטפל במחרוזות נשתמש במחלקה String למחלקה String מתודות שונות שמאפשרות פעולות
תוכנה 1 תרגול מספר 12: GUI כתיבת מחלקות גנריות בית הספר למדעי המחשב אוניברסיטת תל אביב 1
 תוכנה 1 תרגול מספר 12: GUI כתיבת מחלקות גנריות בית הספר למדעי המחשב אוניברסיטת תל אביב 1 2 SWT בנויה על העיקרון של publish/subscribe אלמנטים בסיסיים )Widgets( מייצרים מאזינים )Listener( אירועים )Events(
תוכנה 1 תרגול מספר 12: GUI כתיבת מחלקות גנריות בית הספר למדעי המחשב אוניברסיטת תל אביב 1 2 SWT בנויה על העיקרון של publish/subscribe אלמנטים בסיסיים )Widgets( מייצרים מאזינים )Listener( אירועים )Events(
PowerPoint Presentation
 == vs equals תוכנה תרגול 7 :מנשקים, פולימורפיזם ועוד Point p = new Point(,) Point p = new Point(,) p == p p.equals(p) מתי נכון להשתמש בכל אחד מהם? שימו לב, במחלקה שכתבתם בעצמכם יש לכתוב מתודת equals על
== vs equals תוכנה תרגול 7 :מנשקים, פולימורפיזם ועוד Point p = new Point(,) Point p = new Point(,) p == p p.equals(p) מתי נכון להשתמש בכל אחד מהם? שימו לב, במחלקה שכתבתם בעצמכם יש לכתוב מתודת equals על
PowerPoint Presentation
 תוכנה תרגול 7 :מנשקים, פולימורפיזם ועוד * לא בהכרח בסדר הזה == vs equals Point p = new Point(,2) Point p2 = new Point(,2) p == p2 p.equals(p2) מתי נכון להשתמש בכל אחד מהם? שימו לב, במחלקה שכתבתם בעצמכם
תוכנה תרגול 7 :מנשקים, פולימורפיזם ועוד * לא בהכרח בסדר הזה == vs equals Point p = new Point(,2) Point p2 = new Point(,2) p == p2 p.equals(p2) מתי נכון להשתמש בכל אחד מהם? שימו לב, במחלקה שכתבתם בעצמכם
מבוא למדעי המחשב
 מבוא למדעי המחשב 202-1-1011 תאריך הבחינה: שמות המרצים: 16.3.2011 מר שי זקוב ד"ר פז כרמי פרופ' מייק קודיש ד"ר חן קיסר ד"ר צחי רוזן שם הקורס: מבוא למדעי המחשב מספר הקורס: שנה: 202-1-1011 2011 משך הבחינה:
מבוא למדעי המחשב 202-1-1011 תאריך הבחינה: שמות המרצים: 16.3.2011 מר שי זקוב ד"ר פז כרמי פרופ' מייק קודיש ד"ר חן קיסר ד"ר צחי רוזן שם הקורס: מבוא למדעי המחשב מספר הקורס: שנה: 202-1-1011 2011 משך הבחינה:
שאלהIgal : מערכים דו מימדיים רקורסיה:
 אוניברסיטת בן גוריון בנגב מספר נבחן : תאריך המבחן: כ"ג מנ' אב תשע"ז 15.08.17 שמות המורים: ציון סיקסיק א' ב- C תכנות מבחן ב: 202-1-9011 מס' הקורס : הנדסה מיועד לתלמידי : ב' מועד סמ' ב' שנה תשע"ז 3 שעות
אוניברסיטת בן גוריון בנגב מספר נבחן : תאריך המבחן: כ"ג מנ' אב תשע"ז 15.08.17 שמות המורים: ציון סיקסיק א' ב- C תכנות מבחן ב: 202-1-9011 מס' הקורס : הנדסה מיועד לתלמידי : ב' מועד סמ' ב' שנה תשע"ז 3 שעות
מהוא לתכנות ב- JAVA מעבדה 3
 מבוא לתכנות ב- JAVA מעבדה 3 נושאי התרגול לולאות ניפוי שגיאות לולאות - הקדמה כיצד הייתם כותבים תוכנית שתדפיס את המספרים השלמים בין 1 ל- 100 בעזרת הכלים שלמדתם עד עתה? חייבת להיות דרך אחרת מאשר לכתוב 100
מבוא לתכנות ב- JAVA מעבדה 3 נושאי התרגול לולאות ניפוי שגיאות לולאות - הקדמה כיצד הייתם כותבים תוכנית שתדפיס את המספרים השלמים בין 1 ל- 100 בעזרת הכלים שלמדתם עד עתה? חייבת להיות דרך אחרת מאשר לכתוב 100
תכנות מונחה עצמים א' – תש"ע
 1 תכנות מונחה עצמים והנדסת תוכנה תשע"ו 2 בנאי העתקה בניית העתק של אובייקט קיים. בניית העתק בעת העברת אובייקט לפונקציה. בניית העתק בעת החזרת אובייקט מפונקציה. ניתן להגדיר בנאי העתקה. אם לא מגדירים, אז הקומפיילר
1 תכנות מונחה עצמים והנדסת תוכנה תשע"ו 2 בנאי העתקה בניית העתק של אובייקט קיים. בניית העתק בעת העברת אובייקט לפונקציה. בניית העתק בעת החזרת אובייקט מפונקציה. ניתן להגדיר בנאי העתקה. אם לא מגדירים, אז הקומפיילר
מבנים בדידים וקומבינטוריקה סמסטר אביב תשע"ט מספרי רמזי תרגול 11 הגדרה: (t R = R(s, הוא המספר הטבעי הקטן ביותר כך שבכל צביעה של צלעות הגרף וכחול(, קיים
 מספרי רמזי תרגול 11 הגדרה: (t R = R(s הוא המספר הטבעי הקטן ביותר כך שבכל צביעה של צלעות הגרף וכחול( קיים תת-גרף שלם K s שצבוע בכחול או שקיים תת-גרף שלם K t שצבוע באדום. הגדרה שקולה: עבור גרף עם לפחות (t
מספרי רמזי תרגול 11 הגדרה: (t R = R(s הוא המספר הטבעי הקטן ביותר כך שבכל צביעה של צלעות הגרף וכחול( קיים תת-גרף שלם K s שצבוע בכחול או שקיים תת-גרף שלם K t שצבוע באדום. הגדרה שקולה: עבור גרף עם לפחות (t
Microsoft Word - pitaron222Java_2007.doc
 1 מדעי המחשב 2 יחידות לימוד פתרון בחינת הבגרות פרק א a mul k k a פלט b זוגי? b :1 Ï 3 1 5 1 5 F קלט: 3, 5, 8, 4 20 2 8 40 40 3 4 4 F :2 Ï m x x 0 פלט 70 x 50 0 א. 10 F 1 64 2 2 51 30 F -4 F ב. ג. 1- (כל
1 מדעי המחשב 2 יחידות לימוד פתרון בחינת הבגרות פרק א a mul k k a פלט b זוגי? b :1 Ï 3 1 5 1 5 F קלט: 3, 5, 8, 4 20 2 8 40 40 3 4 4 F :2 Ï m x x 0 פלט 70 x 50 0 א. 10 F 1 64 2 2 51 30 F -4 F ב. ג. 1- (כל
משימה תכנית המתרגמת קטעי טקסט לשפה אחרת הקלט: קובץ המכיל את קטעי הטקסט וכן את השפה אליה רוצים לתרגם תרגול מס' 4: המתרגם שימוש במחלקות קיימות תכנות מתק
 משימה תכנית המתרגמת קטעי טקסט לשפה אחרת הקלט: קובץ המכיל את קטעי הטקסט וכן את השפה אליה רוצים לתרגם תרגול מס' 4: המתרגם שימוש במחלקות קיימות 2 הפשטה שאלות כצעד ראשון נפתור בעיה הרבה יותר פשוטה האם כבר
משימה תכנית המתרגמת קטעי טקסט לשפה אחרת הקלט: קובץ המכיל את קטעי הטקסט וכן את השפה אליה רוצים לתרגם תרגול מס' 4: המתרגם שימוש במחלקות קיימות 2 הפשטה שאלות כצעד ראשון נפתור בעיה הרבה יותר פשוטה האם כבר
PowerPoint Presentation
 תוכנה 1 תרגול 1: סביבת העבודה ומבוא ל- Java 1 מנהלות אתר הקורס: http://courses.cs.tau.ac.il/software1/1516b/ מתרגלים: ברית יונגמן )שעת קבלה: שלישי ב- 8:00 בתיאום מראש( לנה דנקין )שעת קבלה: שלישי ב- 17:00,
תוכנה 1 תרגול 1: סביבת העבודה ומבוא ל- Java 1 מנהלות אתר הקורס: http://courses.cs.tau.ac.il/software1/1516b/ מתרגלים: ברית יונגמן )שעת קבלה: שלישי ב- 8:00 בתיאום מראש( לנה דנקין )שעת קבלה: שלישי ב- 17:00,
מס' סידורי: ת.ז.: עמוד 1 מתוך 20 בחינה בתוכנה 1 סמסטר ב', מועד א',תשס"ט 5/7/2009 וולף, ליאור ליאור שפירא, נעמה מאיר, מתי שמרת הוראות )נא לקרוא!( משך ה
 מס' סידורי: עמוד 1 מתוך 20 בחינה בתוכנה 1 סמסטר ב', מועד א',תשס"ט 5/7/2009 וולף, ליאור ליאור שפירא, נעמה מאיר, מתי שמרת הוראות )נא לקרוא!( משך הבחינה שלוש שעות - חלקו את זמנכם ביעילות. יש לענות על כל השאלות.
מס' סידורי: עמוד 1 מתוך 20 בחינה בתוכנה 1 סמסטר ב', מועד א',תשס"ט 5/7/2009 וולף, ליאור ליאור שפירא, נעמה מאיר, מתי שמרת הוראות )נא לקרוא!( משך הבחינה שלוש שעות - חלקו את זמנכם ביעילות. יש לענות על כל השאלות.
Microsoft PowerPoint - rec3.ppt
 תכנו ת מונח ה עצ מים משתני מחלקה, עצמים מוכלים ועצמים מוצבעים א וה ד ברז יל י א ונ יברס י ט ת תל אביב משתנ י מח ל קה Static Members משתני מחלקה members) (static משתנים סטטיים מוגדרי ם בתוך מח לקה ואולם
תכנו ת מונח ה עצ מים משתני מחלקה, עצמים מוכלים ועצמים מוצבעים א וה ד ברז יל י א ונ יברס י ט ת תל אביב משתנ י מח ל קה Static Members משתני מחלקה members) (static משתנים סטטיים מוגדרי ם בתוך מח לקה ואולם
Microsoft PowerPoint - 10_threads.ppt
 נוש אים מתקדמים ב Java תכ נות מ ר ובה חו ט י ם אוהד ברזילי אוניברסיטת תל אביב מק בי ל יות ריבוי מעבדים processors) (multi זמן עיבוד slicing) (time ל עו מת חלוק ת רמת התהליך (multithreading) ההפעלה processes)
נוש אים מתקדמים ב Java תכ נות מ ר ובה חו ט י ם אוהד ברזילי אוניברסיטת תל אביב מק בי ל יות ריבוי מעבדים processors) (multi זמן עיבוד slicing) (time ל עו מת חלוק ת רמת התהליך (multithreading) ההפעלה processes)
מבחן סוף סמסטר מועד ב 28/10/08 מרצה אחראית: דר שירלי הלוי גינסברג מתרגלים: גלעד קותיאל, גדי אלכסנדרוביץ הוראות: א. בטופס המבחן 6 עמודים (כולל דף זה) ו
 מבחן סוף סמסטר מועד ב 28/10/08 מרצה אחראית: דר שירלי הלוי גינסברג מתרגלים: גלעד קותיאל, גדי אלכסנדרוביץ הוראות: א. בטופס המבחן 6 עמודים (כולל דף זה) ו 4 דפי נוסחאות. בדקו שכל העמודים ברשותכם. ב. משך המבחן
מבחן סוף סמסטר מועד ב 28/10/08 מרצה אחראית: דר שירלי הלוי גינסברג מתרגלים: גלעד קותיאל, גדי אלכסנדרוביץ הוראות: א. בטופס המבחן 6 עמודים (כולל דף זה) ו 4 דפי נוסחאות. בדקו שכל העמודים ברשותכם. ב. משך המבחן
מועד: א בחינה סופית במתמטיקה דיסקרטית משך הבחינה: 2 1 שעות מרצה: פרופ' תאופיק מנסור תאריך: סמסטר: א תשע"ח m 2 הוראות לנבחן: )1( הבחינה מו
 מועד: א בחינה סופית במתמטיקה דיסקרטית משך הבחינה: 2 1 שעות מרצה: פרופ' תאופיק מנסור תאריך: 26.01.2018 2 סמסטר: א תשע"ח m 2 הוראות לנבחן: )1( הבחינה מורכבת מ- 6 שאלות. כל שאלה מזכה ב- 20 נקודות כך הנקודות
מועד: א בחינה סופית במתמטיקה דיסקרטית משך הבחינה: 2 1 שעות מרצה: פרופ' תאופיק מנסור תאריך: 26.01.2018 2 סמסטר: א תשע"ח m 2 הוראות לנבחן: )1( הבחינה מורכבת מ- 6 שאלות. כל שאלה מזכה ב- 20 נקודות כך הנקודות
Microsoft Word - עבודת פסח לכיתה י 5 יחל.doc
 עבודת פסח במתמטיקה לכיתה י' (5 יחידות) תרגילים שבעבודה על החומר שנלמד בכיתה ומיועדים לחזרה יש לעשות לא פחות מ- תרגילים מכל פרק אלגברה פתור את מערכת המשוואות הבאות: y x 1 y y 1 x y m x 1 x עבור אילו ערכים
עבודת פסח במתמטיקה לכיתה י' (5 יחידות) תרגילים שבעבודה על החומר שנלמד בכיתה ומיועדים לחזרה יש לעשות לא פחות מ- תרגילים מכל פרק אלגברה פתור את מערכת המשוואות הבאות: y x 1 y y 1 x y m x 1 x עבור אילו ערכים
PowerPoint Presentation
 1 תוכנה 1 תרגול 1: מנהלות, סביבת העבודה ומבוא ל- Java 1 2 מנהלות I מתרגלים: יעל אמסטרדמר )שעת קבלה: חמישי ב- 12, בתיאום מראש( דביר נתנאלי )שעת קבלה: רביעי ב- 17, בתיאום מראש( http://courses.cs.tau.ac.il/software1/1415a
1 תוכנה 1 תרגול 1: מנהלות, סביבת העבודה ומבוא ל- Java 1 2 מנהלות I מתרגלים: יעל אמסטרדמר )שעת קבלה: חמישי ב- 12, בתיאום מראש( דביר נתנאלי )שעת קבלה: רביעי ב- 17, בתיאום מראש( http://courses.cs.tau.ac.il/software1/1415a
PowerPoint Presentation
 תוכנה 1 Generics תרגול - 1 תכנות גנרי תמיכה בתכנות גנרי נוספה בגרסה 5 ניתן להגדיר מחלקות ושירותים גנריים מונע שכפול קוד )מוכללים( ניתן לכתוב תוכניות שאינן תלויות בטיפוסי המשתנים מאפשר בטיחות טיפוסים מנגנון
תוכנה 1 Generics תרגול - 1 תכנות גנרי תמיכה בתכנות גנרי נוספה בגרסה 5 ניתן להגדיר מחלקות ושירותים גנריים מונע שכפול קוד )מוכללים( ניתן לכתוב תוכניות שאינן תלויות בטיפוסי המשתנים מאפשר בטיחות טיפוסים מנגנון
תכנות דינמי פרק 6, סעיפים 1-6, ב- Kleinberg/Tardos סכום חלקי מרחק עריכה הרעיון: במקום להרחיב פתרון חלקי יחיד בכל צעד, נרחיב כמה פתרונות אפשריים וניקח
 תכנות דינמי פרק 6, סעיפים -6, ב- Kleinberg/Tardos סכום חלקי מרחק עריכה הרעיון: במקום להרחיב פתרון חלקי יחיד בכל צעד, נרחיב כמה פתרונות אפשריים וניקח בסוף את הטוב ביותר. סכום חלקי sum) (subset הקלט: סדרה
תכנות דינמי פרק 6, סעיפים -6, ב- Kleinberg/Tardos סכום חלקי מרחק עריכה הרעיון: במקום להרחיב פתרון חלקי יחיד בכל צעד, נרחיב כמה פתרונות אפשריים וניקח בסוף את הטוב ביותר. סכום חלקי sum) (subset הקלט: סדרה
Microsoft Word - tutorial Dynamic Programming _Jun_-05.doc
 הטכניון מכון טכנולוגי לישראל אלגוריתמים (3447) סמסטר חורף 006/007 הפקולטה למדעי המחשב תכנון דינאמי תרגיל תת מחרוזת משותפת ארוכה ביותר תת-מחרוזת z k שקיימת סדרה עולה ממש,... z = z של מחרוזת נתונה x m,...,,
הטכניון מכון טכנולוגי לישראל אלגוריתמים (3447) סמסטר חורף 006/007 הפקולטה למדעי המחשב תכנון דינאמי תרגיל תת מחרוזת משותפת ארוכה ביותר תת-מחרוזת z k שקיימת סדרה עולה ממש,... z = z של מחרוזת נתונה x m,...,,
Microsoft Word - c_SimA_MoedB2005.doc
 מרצה: שולי וינטנר. מתרגל: עזרא דאיה. מבוא למדעי המחשב בחינת מועד ב', סמסטר א' תשס"ה,.2.2005 משך המבחן: שעתיים וחצי. חומר עזר: מותר כל חומר עזר, מלבד מחשב. הנחיות:. ודאו כי בטופס שבידיכם עמודים. יש לכתוב
מרצה: שולי וינטנר. מתרגל: עזרא דאיה. מבוא למדעי המחשב בחינת מועד ב', סמסטר א' תשס"ה,.2.2005 משך המבחן: שעתיים וחצי. חומר עזר: מותר כל חומר עזר, מלבד מחשב. הנחיות:. ודאו כי בטופס שבידיכם עמודים. יש לכתוב
פתרון 2000 א. טבלת מעקב אחר ביצוע האלגוריתם הנתון עבור הערכים : פלט num = 37, sif = 7 r האם ספרת האחדות של sif שווה ל- num num 37 sif 7 שורה (1)-(2) (
 פתרון 000 א. טבלת מעקב אחר ביצוע האלגוריתם הנתון עבור הערכים : num = 3, sif = r האם ספרת האחדות של sif שווה ל- num num 3 sif (1)-() (3) () אמת ) = ( 3 3 יודפס: 3. ב. פתרון שאלה 11 עבור הערכים: עבור סעיף
פתרון 000 א. טבלת מעקב אחר ביצוע האלגוריתם הנתון עבור הערכים : num = 3, sif = r האם ספרת האחדות של sif שווה ל- num num 3 sif (1)-() (3) () אמת ) = ( 3 3 יודפס: 3. ב. פתרון שאלה 11 עבור הערכים: עבור סעיף
תשובות מלאות לבחינת הבגרות במתמטיקה מועד ג' תשע"ד, מיום 0/8/0610 שאלונים: 313, מוצע על ידי בית הספר לבגרות ולפסיכומטרי של אבירם פלדמן שאלה מספר
 תשובות מלאות לבחינת הבגרות במתמטיקה מועד ג' תשע"ד, מיום 0/8/0610 שאלונים: 313, 635863 מוצע על ידי בית הספר לבגרות ולפסיכומטרי של אבירם פלדמן שאלה מספר 1 נתון: 1 תלמיד קנה 11 מחברות דקות ו- 4 מחברות עבות,
תשובות מלאות לבחינת הבגרות במתמטיקה מועד ג' תשע"ד, מיום 0/8/0610 שאלונים: 313, 635863 מוצע על ידי בית הספר לבגרות ולפסיכומטרי של אבירם פלדמן שאלה מספר 1 נתון: 1 תלמיד קנה 11 מחברות דקות ו- 4 מחברות עבות,
PowerPoint Presentation
 תוכנה 1 3 תרגול מס' מתודות ותיכון לפי חוזים חוזה בין ספק ללקוח חוזה בין ספק ללקוח מגדיר עבור כל שרות: תנאי ללקוח - "תנאי קדם" precondition - - תנאי לספק "תנאי אחר".postcondition לקוח ספק 2 תנאי קדם )preconditions(
תוכנה 1 3 תרגול מס' מתודות ותיכון לפי חוזים חוזה בין ספק ללקוח חוזה בין ספק ללקוח מגדיר עבור כל שרות: תנאי ללקוח - "תנאי קדם" precondition - - תנאי לספק "תנאי אחר".postcondition לקוח ספק 2 תנאי קדם )preconditions(
תרגול מס' 7 – חזרה על MST ואלגוריתם Dijkstra
 תרגול מס' 10 תכנון ליניארי תכנון לינארי הינו כלי שימושי במדעי המחשב. בקורס ראינו כיצד ניתן להציג בעיות שונות במסגרת תכנון לינארי. בנוסף, ראינו שימושים לדואליות של תוכניות לינאריות, אשר מקשרת בין בעיות
תרגול מס' 10 תכנון ליניארי תכנון לינארי הינו כלי שימושי במדעי המחשב. בקורס ראינו כיצד ניתן להציג בעיות שונות במסגרת תכנון לינארי. בנוסף, ראינו שימושים לדואליות של תוכניות לינאריות, אשר מקשרת בין בעיות
Microsoft Word - Questions Booklet Spring 2009
 אלגוריתמים 1 חוברת תרגילים נא לשלוח כל הערה לגיל כהן במייל cohen@cs.technion.ac.il מפתח שאלות לפי נושאים 1, 45, 54, 55, 56, 76 5, 63 :BFS :DFS מיון טופולוגי: 17, 31, 32, 57, 67, 68 2, 25, 26, 28, 50 21,
אלגוריתמים 1 חוברת תרגילים נא לשלוח כל הערה לגיל כהן במייל cohen@cs.technion.ac.il מפתח שאלות לפי נושאים 1, 45, 54, 55, 56, 76 5, 63 :BFS :DFS מיון טופולוגי: 17, 31, 32, 57, 67, 68 2, 25, 26, 28, 50 21,
תרגול מס' 7: תרגילים מתקדמים ברקורסיה
 תרגול מס' :7,Memoization Quicksort ותרגילים מתקדמים ברקורסיה תרגול זה הוא התרגול האחרון שיהיה לכם בנושא רקורסיה והוא מכיל מגוון שאלות מתקדמות בנשוא זה. השאלות שיכלול תרגול זה: Memoization פיבונאצ'י Quicksort
תרגול מס' :7,Memoization Quicksort ותרגילים מתקדמים ברקורסיה תרגול זה הוא התרגול האחרון שיהיה לכם בנושא רקורסיה והוא מכיל מגוון שאלות מתקדמות בנשוא זה. השאלות שיכלול תרגול זה: Memoization פיבונאצ'י Quicksort
PowerPoint Presentation
 תרגול מס' 4: המתרגם שימוש במחלקות קיימות מחרוזות, קבצים, וקבלת קלט מהמשתמש המתרגם משימה: תכנית המתרגמת קטעי טקסט לשפה אחרת הקלט: קובץ המכיל את קטעי הטקסט וכן את השפה אליה רוצים לתרגם 2 שאלות האם כבר יש
תרגול מס' 4: המתרגם שימוש במחלקות קיימות מחרוזות, קבצים, וקבלת קלט מהמשתמש המתרגם משימה: תכנית המתרגמת קטעי טקסט לשפה אחרת הקלט: קובץ המכיל את קטעי הטקסט וכן את השפה אליה רוצים לתרגם 2 שאלות האם כבר יש
מקביליות
 PROMELA גרא וייס המחלקה למדעי המחשב אוניברסיטת בן-גוריון עדכון אחרון: 21:40 15/06/2013 2 שפת מ פ ר ט עם ס מ נ ט יק ה מוגדרת באופן מתמטי "שפת תכנות" למודלים המטרה: לאפשר גם לכאלה שאינם חוקרים בתחום לבנות
PROMELA גרא וייס המחלקה למדעי המחשב אוניברסיטת בן-גוריון עדכון אחרון: 21:40 15/06/2013 2 שפת מ פ ר ט עם ס מ נ ט יק ה מוגדרת באופן מתמטי "שפת תכנות" למודלים המטרה: לאפשר גם לכאלה שאינם חוקרים בתחום לבנות
סדנת תכנות ב C/C++
 פקולטה: מדעי הטבע מחלקה: מדעי המחשב שם הקורס: מבוא למחשבים ושפת C קוד הקורס: 2-7028510 תאריך בחינה: 15.2.2017 משך הבחינה: שעתיים שם המרצה: ד"ר אופיר פלא חומר עזר: פתוח שימוש במחשבון: לא הוראות כלליות:
פקולטה: מדעי הטבע מחלקה: מדעי המחשב שם הקורס: מבוא למחשבים ושפת C קוד הקורס: 2-7028510 תאריך בחינה: 15.2.2017 משך הבחינה: שעתיים שם המרצה: ד"ר אופיר פלא חומר עזר: פתוח שימוש במחשבון: לא הוראות כלליות:
תכנון אלגוריתמים, אביב 1021, תרגול מס' 4 תכנון דינאמי תכנון דינאמי בתרגול זה נדון בבעיית הכפלת סדרת מטריצות (16.1.(CLR ראשית נראה דוגמא: דוגמא: תהינה
 תכנון דינאמי בתרגול זה נדון בבעיית הכפלת סדרת מטריצות (6..(CLR ראשית נראה דוגמא: דוגמא: תהינה ארבע מטריצות:. A, A, A, A נסמן את גודל המטריצות בסדרה ע"י סדרת גדלים כאשר, p 5 5 p היא בגודל A {,,,5,}, P כלומר
תכנון דינאמי בתרגול זה נדון בבעיית הכפלת סדרת מטריצות (6..(CLR ראשית נראה דוגמא: דוגמא: תהינה ארבע מטריצות:. A, A, A, A נסמן את גודל המטריצות בסדרה ע"י סדרת גדלים כאשר, p 5 5 p היא בגודל A {,,,5,}, P כלומר
1
 תאריך הבחינה: 24.7.2016. שמות המרצים: ד"ר עזאם מרעי שם הקורס: עקרונות תכנות מונחה עצמים מספר הקורס: 202-15181 שנה: 2016 סמסטר: ב' מועד: א' משך הבחינה: שלוש שעות חומר עזר: אסור מבחן סיכום לקורס " עקרונות
תאריך הבחינה: 24.7.2016. שמות המרצים: ד"ר עזאם מרעי שם הקורס: עקרונות תכנות מונחה עצמים מספר הקורס: 202-15181 שנה: 2016 סמסטר: ב' מועד: א' משך הבחינה: שלוש שעות חומר עזר: אסור מבחן סיכום לקורס " עקרונות
PowerPoint Presentation
 מבוא למדעי המחשב תירגול 6: כתובות ומצביעים 1 תוכנייה מצביעים מצביעים ומערכים, אריתמטיקה של מצביעים 2 3 מצביעים תזכורת- כתובות זיכרון הזיכרון כתובת התא #1000 #1004 #1008 ערך השמור בתא תא 10-4 לא מאותחל
מבוא למדעי המחשב תירגול 6: כתובות ומצביעים 1 תוכנייה מצביעים מצביעים ומערכים, אריתמטיקה של מצביעים 2 3 מצביעים תזכורת- כתובות זיכרון הזיכרון כתובת התא #1000 #1004 #1008 ערך השמור בתא תא 10-4 לא מאותחל
עבודת בית מספר 5: מבני נתונים מבוא למדעי המחשב, סמסטר א' תשע"ט מבוא למדעי המחשב סמסטר א' תשע"ט צוות העבודה: מרצה אחראי: יוחאי טוויטו מתרגלים אחראים: א
 מבוא למדעי המחשב סמסטר א' תשע"ט צוות העבודה: מרצה אחראי: יוחאי טוויטו מתרגלים אחראים: אופיר גגולשוילי, ירין קופר תאריך פרסום: 20.12.18 תאריך הגשה: 12:00 3.1.18, בצהריים. הוראות מקדימות הגשת עבודות בית
מבוא למדעי המחשב סמסטר א' תשע"ט צוות העבודה: מרצה אחראי: יוחאי טוויטו מתרגלים אחראים: אופיר גגולשוילי, ירין קופר תאריך פרסום: 20.12.18 תאריך הגשה: 12:00 3.1.18, בצהריים. הוראות מקדימות הגשת עבודות בית
תוכן העניינים
 הוצאת חושבים קדימה הילה קדמן חלק ב יעוץ מקצועי: חיים אברבוך מותאם לתכנית הלימודים החדשה בבתי הספר התיכוניים מהדורה חמישית הוצאת חושבים קדימה ת.ד. 1293 רעות 71908 www.kadman.net הילה קדמן 0522 525527 kadman11@gmail.com
הוצאת חושבים קדימה הילה קדמן חלק ב יעוץ מקצועי: חיים אברבוך מותאם לתכנית הלימודים החדשה בבתי הספר התיכוניים מהדורה חמישית הוצאת חושבים קדימה ת.ד. 1293 רעות 71908 www.kadman.net הילה קדמן 0522 525527 kadman11@gmail.com
תרגול 3 - מערכים
 Introduction to Programming in Java תרגול 5 1 היום בתרגול void מה הן פונקציות הגדרת פונקציה, קריאה לפונקציה העברת ארגומנטים, החזרת ערך או דוגמאות 2 מוטיבציה לעיתים,אנו נזקקים לבצע פעולה מסוימת או לעשות
Introduction to Programming in Java תרגול 5 1 היום בתרגול void מה הן פונקציות הגדרת פונקציה, קריאה לפונקציה העברת ארגומנטים, החזרת ערך או דוגמאות 2 מוטיבציה לעיתים,אנו נזקקים לבצע פעולה מסוימת או לעשות
Microsoft Word a_moed_a_solution.doc
 עמוד 1 מתוך 18 פתרון הבחינה בתוכנה 1 אוהד ברזילי, סיון טולדו, מיכל עוזרי-פלאטו, ליאור שפירא מועד א' סמסטר א' תשס"ז, 11 בפברואר 2007 משך הבחינה שלוש שעות. יש לענות על כל השאלות. בשאלות שבהן יש צורך לנמק,
עמוד 1 מתוך 18 פתרון הבחינה בתוכנה 1 אוהד ברזילי, סיון טולדו, מיכל עוזרי-פלאטו, ליאור שפירא מועד א' סמסטר א' תשס"ז, 11 בפברואר 2007 משך הבחינה שלוש שעות. יש לענות על כל השאלות. בשאלות שבהן יש צורך לנמק,
מבוא למדעי המחשב - חובלים
 אוניברסיטת חיפה החוג למדעי המחשב מבוא למדעי המחשב סמסטר ב' תשע"ב בחינת סיום, מועד ב',.02..9.7 מרצה: אורן וימן מתרגלים: נעמה טוויטו ועדו ניסנבוים מדריכי מעבדה: מחמוד שריף ומיקה עמית משך המבחן: שעתיים חומר
אוניברסיטת חיפה החוג למדעי המחשב מבוא למדעי המחשב סמסטר ב' תשע"ב בחינת סיום, מועד ב',.02..9.7 מרצה: אורן וימן מתרגלים: נעמה טוויטו ועדו ניסנבוים מדריכי מעבדה: מחמוד שריף ומיקה עמית משך המבחן: שעתיים חומר
תאריך פרסום: תאריך הגשה: מבנה נתונים תרגיל 5 )תיאורטי( מרצה ומתרגל אחראים: צחי רוזן, דינה סבטליצקי נהלי הגשת עבודה: -את העבודה יש לה
 תאריך פרסום: 01.01.15 תאריך הגשה: 15.01.15 מבנה נתונים תרגיל 5 )תיאורטי( מרצה ומתרגל אחראים: צחי רוזן, דינה סבטליצקי נהלי הגשת עבודה: -את העבודה יש להגיש בזוגות. -העבודה חייבת להיות מוקלדת. -הקובץ חייב
תאריך פרסום: 01.01.15 תאריך הגשה: 15.01.15 מבנה נתונים תרגיל 5 )תיאורטי( מרצה ומתרגל אחראים: צחי רוזן, דינה סבטליצקי נהלי הגשת עבודה: -את העבודה יש להגיש בזוגות. -העבודה חייבת להיות מוקלדת. -הקובץ חייב
1 בגרות עח יולי 18 מועד קיץ ב שאלון x b 2 2 y x 6x שיעור ה- א x לכן, של קדקוד הפרבולה, ו-, מתקבל על ידי הנוסחה a. C(3, 9) ובהתאם, y. (3, 9) 2 C
 8 מועד קיץ ב שאלון 58 x b y x x שיעור ה- א x לכן של קדקוד הפרבולה ו- מתקבל על ידי הנוסחה a C( 9) ובהתאם y ( 9) C 9 C הם x C ( ) תשובה: שיעורי קדקוד הפרבולה B A y x x ב הישר y 5 חותך את הפרבולה בנקודות
8 מועד קיץ ב שאלון 58 x b y x x שיעור ה- א x לכן של קדקוד הפרבולה ו- מתקבל על ידי הנוסחה a C( 9) ובהתאם y ( 9) C 9 C הם x C ( ) תשובה: שיעורי קדקוד הפרבולה B A y x x ב הישר y 5 חותך את הפרבולה בנקודות
Tutorial 11
 מבוא לשפת C תרגול 8: מערכים רב-ממדיים תרגילים בנושא מערכים ורקורסיה מבוסס על השקפים שחוברו ע"י שי ארצי, גיתית רוקנשטיין, איתן אביאור וסאהר אסמיר עבור הקורס "מבוא למדעי המחשב" נכתב ע"י טל כהן, עודכן ע"י
מבוא לשפת C תרגול 8: מערכים רב-ממדיים תרגילים בנושא מערכים ורקורסיה מבוסס על השקפים שחוברו ע"י שי ארצי, גיתית רוקנשטיין, איתן אביאור וסאהר אסמיר עבור הקורס "מבוא למדעי המחשב" נכתב ע"י טל כהן, עודכן ע"י
שאלהIgal : מערכים דו מימדיים רקורסיה:
 אוניברסיטת בן גוריון בנגב מספר נבחן : תאריך המבחן: כ"ג חשון תשע"ח 12/11/17 שמות המורים: ציון סיקסיק א' ב- C תכנות מבחן ב: 202-1-9011 מס' הקורס : הנדסה מיועד לתלמידי : ב' מועד קיץ סמ' שנה תשע"ז 3 שעות משך
אוניברסיטת בן גוריון בנגב מספר נבחן : תאריך המבחן: כ"ג חשון תשע"ח 12/11/17 שמות המורים: ציון סיקסיק א' ב- C תכנות מבחן ב: 202-1-9011 מס' הקורס : הנדסה מיועד לתלמידי : ב' מועד קיץ סמ' שנה תשע"ז 3 שעות משך
שאלהIgal : מערכים דו מימדיים רקורסיה:
 אוניברסיטת בן גוריון בנגב מספר נבחן : תאריך המבחן: כ"ח תשרי תשע"ז 30.10.16 שמות המורים: ציון סיקסיק א' תכנות ב- C מבחן ב: 202-1-9011 מס' הקורס : הנדסה מיועד לתלמידי : ב' מועד סמ' קיץ שנה תשע"ו 3 שעות משך
אוניברסיטת בן גוריון בנגב מספר נבחן : תאריך המבחן: כ"ח תשרי תשע"ז 30.10.16 שמות המורים: ציון סיקסיק א' תכנות ב- C מבחן ב: 202-1-9011 מס' הקורס : הנדסה מיועד לתלמידי : ב' מועד סמ' קיץ שנה תשע"ו 3 שעות משך
תורת החישוביות תרגול הכנה לוגיקה ותורת הקבוצות מה יש כאן? בקורס תורת החישוביות נניח ידע בסיסי בתורת הקבוצות ובלוגיקה, והכרות עם מושגים בסיסיים כמו א"ב
 תורת החישוביות תרגול הכנה לוגיקה ותורת הקבוצות מה יש כאן? בקורס תורת החישוביות נניח ידע בסיסי בתורת הקבוצות ובלוגיקה, והכרות עם מושגים בסיסיים כמו א"ב, מילה ושפה לטובת מי ששכח חומר זה, או שלא למדו מעולם,
תורת החישוביות תרגול הכנה לוגיקה ותורת הקבוצות מה יש כאן? בקורס תורת החישוביות נניח ידע בסיסי בתורת הקבוצות ובלוגיקה, והכרות עם מושגים בסיסיים כמו א"ב, מילה ושפה לטובת מי ששכח חומר זה, או שלא למדו מעולם,
תורת הקומפילציה
 תורת הקומפילציה תרגיל בית 2 הוראות לתרגיל 2 בשפת MINI-PASCAL הפרוייקט המצורף הינו קוד שלד של מהדר לשפת mini-pascal עליכם לממש בסביבת (Eclipse (Java את הפונקציות המתאימות לפי החומר שנלמד בהרצאה ע"מ שהמהדר
תורת הקומפילציה תרגיל בית 2 הוראות לתרגיל 2 בשפת MINI-PASCAL הפרוייקט המצורף הינו קוד שלד של מהדר לשפת mini-pascal עליכם לממש בסביבת (Eclipse (Java את הפונקציות המתאימות לפי החומר שנלמד בהרצאה ע"מ שהמהדר
תוכן העניינים: פרק צמצומים ומימושים של פונקציות בוליאניות... 2 צמצומים של פונקציות באמצעות מפת קרנו:...2 שאלות:... 2 תשובות סופיות:... 4 צמצום
 תוכן העניינים: פרק 2 3 צמצומים ומימושים של פונקציות בוליאניות 2 צמצומים של פונקציות באמצעות מפת קרנו: 2 שאלות: 2 תשובות סופיות: 4 צמצום באמצעות שיטת 6:QM שאלות: 6 תשובות סופיות: 7 מימושים בעזרת פונקציות
תוכן העניינים: פרק 2 3 צמצומים ומימושים של פונקציות בוליאניות 2 צמצומים של פונקציות באמצעות מפת קרנו: 2 שאלות: 2 תשובות סופיות: 4 צמצום באמצעות שיטת 6:QM שאלות: 6 תשובות סופיות: 7 מימושים בעזרת פונקציות
יחידה 8: שיקוף, הרחבה וכיווץ של פרבולות שיעור 1. שיקוף בציר x תלמידים התבקשו לשרטט פרבולה שכל הערכים שלה שליליים. y יואב ש רטט כך: y תומר אמר: אי-אפשר
 יחידה 8: שיקוף, הרחבה וכיווץ של פרבולות שיעור 1. שיקוף בציר תלמידים התבקשו לשרטט פרבולה שכל הערכים שלה שליליים. יואב ש רטט כך: תומר אמר: אי-אפשר זיו ש רטט כך: מי צודק? נשקף בציר את הגרף של, = ונלמד את
יחידה 8: שיקוף, הרחבה וכיווץ של פרבולות שיעור 1. שיקוף בציר תלמידים התבקשו לשרטט פרבולה שכל הערכים שלה שליליים. יואב ש רטט כך: תומר אמר: אי-אפשר זיו ש רטט כך: מי צודק? נשקף בציר את הגרף של, = ונלמד את
תיק משימטיקה מגרף הנגזרת לגרף הפונקציה להנגשה פרטנית נא לפנות: כל הזכויות שמורות
 תיק משימטיקה מגרף הנגזרת לגרף הפונקציה להנגשה פרטנית נא לפנות: st.negishut@weizmann.ac.il תוכן העניינים מטרות התיק... 3 זמני עבודה משוערים... 3 החומרים והעזרים הדרושים... 4 רקע... 5 הצעה למהלך העבודה...
תיק משימטיקה מגרף הנגזרת לגרף הפונקציה להנגשה פרטנית נא לפנות: st.negishut@weizmann.ac.il תוכן העניינים מטרות התיק... 3 זמני עבודה משוערים... 3 החומרים והעזרים הדרושים... 4 רקע... 5 הצעה למהלך העבודה...
מבוא למדעי המחשב - חובלים
 החוג למדעי המחשב אוניברסיטת חיפה מבוא למדעי המחשב סמסטר א' תשע"ג בחינת סיום, מועד ב', 20.02.2013 מרצה: ריטה אוסדצ'י מתרגלת: נעמה טוויטו מדריך מעבדה: מחמוד שריף משך המבחן: שעתיים חומר עזר: ספר של Kernighan
החוג למדעי המחשב אוניברסיטת חיפה מבוא למדעי המחשב סמסטר א' תשע"ג בחינת סיום, מועד ב', 20.02.2013 מרצה: ריטה אוסדצ'י מתרגלת: נעמה טוויטו מדריך מעבדה: מחמוד שריף משך המבחן: שעתיים חומר עזר: ספר של Kernighan
יוםשישי 14 בספטמבר 2012 ) תכנות מונחה עצמים ( מבחן סוף סמסטר סמסטר אביב 2012, מועד ב' מרצה: קרן לנץ מתרגלים: אייל מושקוביץ, ערן גלעד, ניר האוזר
 יוםשישי 14 בספטמבר 2012 ) תכנות מונחה עצמים ( 236703 מבחן סוף סמסטר סמסטר אביב 2012, מועד ב' מרצה: קרן לנץ מתרגלים: אייל מושקוביץ, ערן גלעד, ניר האוזר הנחיות: במבחן 5 שאלות שוות משקל. עליכם לענות על כל
יוםשישי 14 בספטמבר 2012 ) תכנות מונחה עצמים ( 236703 מבחן סוף סמסטר סמסטר אביב 2012, מועד ב' מרצה: קרן לנץ מתרגלים: אייל מושקוביץ, ערן גלעד, ניר האוזר הנחיות: במבחן 5 שאלות שוות משקל. עליכם לענות על כל
PowerPoint Presentation
 תוכנה 1 אוניברסיטת תל אביב INTERFACES תרגול מס' 7: מנשקים, פולימורפיזם ועוד * לא בהכרח בסדר הזה מנשקים )Interfaces( 2 מנשקים מנשק )interface( הוא מבנה תחבירי ב- Java המאפשר לחסוך בקוד לקוח. מנשק מכיל כותרות
תוכנה 1 אוניברסיטת תל אביב INTERFACES תרגול מס' 7: מנשקים, פולימורפיזם ועוד * לא בהכרח בסדר הזה מנשקים )Interfaces( 2 מנשקים מנשק )interface( הוא מבנה תחבירי ב- Java המאפשר לחסוך בקוד לקוח. מנשק מכיל כותרות
מספר מחברת: עמוד 1 מתוך 11 ת"ז: תשע"א מועד ב סמסטר א' תאריך: 00:11 שעה: 0 שעות הבחינה: משך כל חומר עזר אסור בשימוש בחינה בקורס: מבוא למדעי ה
 עמוד 1 מתוך 11 תשע"א מועד ב סמסטר א' 14.2.2011 תאריך: 00:11 שעה: 0 שעות הבחינה: משך כל חומר עזר אסור בשימוש בחינה בקורס: מבוא למדעי המחשב יש לענות על כל 5 השאלות. בכל השאלות במבחן יש לכתוב פונקציות יעילות
עמוד 1 מתוך 11 תשע"א מועד ב סמסטר א' 14.2.2011 תאריך: 00:11 שעה: 0 שעות הבחינה: משך כל חומר עזר אסור בשימוש בחינה בקורס: מבוא למדעי המחשב יש לענות על כל 5 השאלות. בכל השאלות במבחן יש לכתוב פונקציות יעילות
Slide 1
 שיעור מספר 7: "אמא יש רק אחת" )הורשה I( שחר מעוז בית הספר למדעי המחשב על סדר היום יחסים בין מחלקות ירושה כיחס is-a טיפוס סטטי וטיפוס דינמי המחלקה Object מחלקות מופשטות 2 מלבן צבעוני נרצה לבנות מחלקה המייצגת
שיעור מספר 7: "אמא יש רק אחת" )הורשה I( שחר מעוז בית הספר למדעי המחשב על סדר היום יחסים בין מחלקות ירושה כיחס is-a טיפוס סטטי וטיפוס דינמי המחלקה Object מחלקות מופשטות 2 מלבן צבעוני נרצה לבנות מחלקה המייצגת
Slide 1
 מבוא למדעי המחשב תירגול 4: משתנים בוליאניים ופונקציות מבוא למדעי המחשב מ' - תירגול 4 1 משתנים בוליאניים מבוא למדעי המחשב מ' - תירגול 4 2 ערכי אמת מבחינים בין שני ערכי אמת: true ו- false לכל מספר שלם ניתן
מבוא למדעי המחשב תירגול 4: משתנים בוליאניים ופונקציות מבוא למדעי המחשב מ' - תירגול 4 1 משתנים בוליאניים מבוא למדעי המחשב מ' - תירגול 4 2 ערכי אמת מבחינים בין שני ערכי אמת: true ו- false לכל מספר שלם ניתן
Microsoft PowerPoint - lec10.ppt
 תכנו ת מ ונחה ע צמ י ם בשפת ++C אוהד ברזילי אוניברסיטת תל אביב ירו ש ה מרו בה המצגת מכילה קטעים מתוך מצגת של פרופ' עמירם יהודאי ע"פ הספר: Object-Oriented Software Construction, 2nd edition, by Bertrand
תכנו ת מ ונחה ע צמ י ם בשפת ++C אוהד ברזילי אוניברסיטת תל אביב ירו ש ה מרו בה המצגת מכילה קטעים מתוך מצגת של פרופ' עמירם יהודאי ע"פ הספר: Object-Oriented Software Construction, 2nd edition, by Bertrand
מבוא למדעי המחשב, סמסטר א', תשס"ח תרגול מס' 2
 מבוא למדעי המחשב תרגול מס' 2 נושאים משתנים טיפוסים אופרטורים פונקציות מתמטיות מהמחלקה Math המרת טיפוסים תנאים ולולאות 1 2 תזכורת משיעור קודם תזכורת... תכנית מחשב נכתבת כטקסט בקובץ. הטקסט כתוב בשפת תכנות
מבוא למדעי המחשב תרגול מס' 2 נושאים משתנים טיפוסים אופרטורים פונקציות מתמטיות מהמחלקה Math המרת טיפוסים תנאים ולולאות 1 2 תזכורת משיעור קודם תזכורת... תכנית מחשב נכתבת כטקסט בקובץ. הטקסט כתוב בשפת תכנות
מצגת של PowerPoint
 מבוא כללי לתכנות ולמדעי המחשב תרגול מס' 1 דין שמואל dshmuel110@gmail.com 1 1. מנהלות מרצה: אמיר רובינשטיין, amirr@tau.ac.il שעות קבלה: לשאלות קצרות - מייד לאחר השיעור. ניתן לתאם במייל שעות אחרות. מתרגל:
מבוא כללי לתכנות ולמדעי המחשב תרגול מס' 1 דין שמואל dshmuel110@gmail.com 1 1. מנהלות מרצה: אמיר רובינשטיין, amirr@tau.ac.il שעות קבלה: לשאלות קצרות - מייד לאחר השיעור. ניתן לתאם במייל שעות אחרות. מתרגל:
PowerPoint Presentation
 תרגול מס' 3: המתרגם שימוש במחלקות קיימות מחרוזות, קבצים, וקבלת קלט מהמשתמש שלבי הפיתוח - חזרה קצרה ישנם שני שלבים נפרדים: שלב פיתוח התוכנית בשלב זה אנו משתמשים במהדר )קומפיילר( כדי להמיר קבצי.java )קבצי
תרגול מס' 3: המתרגם שימוש במחלקות קיימות מחרוזות, קבצים, וקבלת קלט מהמשתמש שלבי הפיתוח - חזרה קצרה ישנם שני שלבים נפרדים: שלב פיתוח התוכנית בשלב זה אנו משתמשים במהדר )קומפיילר( כדי להמיר קבצי.java )קבצי
